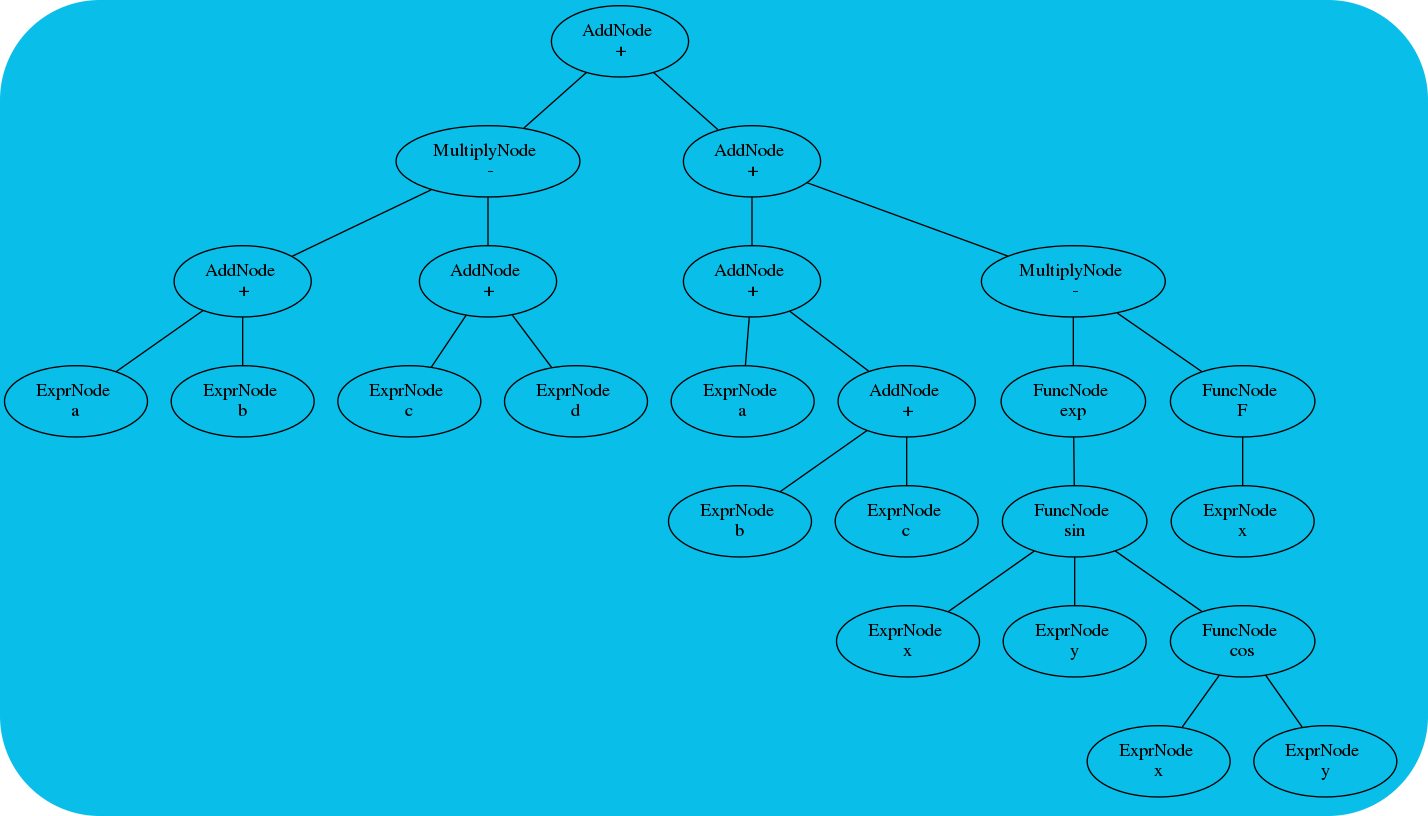

This project was created to satisfy a desire to play around with basic, niche computer algebra concepts. At the most basic level, this project aims to allow the translation of a string of text containing one or more mathematical instructions into an evaluable function (or functions.) In other words: a generic Computer Algebra System (CAS).
The original idea began during a quantum field theory course in which I wrote a (fairly awful) program that could compute tree-level Feyman diagrams directly from a Lagrangian (and some other knowledge about the permitted interactions). Having a little bit of experience with the Maxima CAS (which works *great* when you can figure out how to tell it what you want; I have a special fondness for the Risch algorithm-based integration and Grassmann Algebra facilities of Maxima!) I decided it would be neat to try write my own system. The primary motivation was improving simplification of the algebraic results. So the core focus of this CAS engine is in expression graph re-writing, simplification, and pattern recognition.
My major goal was not to (attempt) to replace existing CAS systems, but rather to learn something about how to implement a parse-optimize-execute cycle in an embedded setting. “Embedded” here refers not to embedded hardware, but an embedded CAS engine: PolyCAS is meant to be used as a library for easily inserting CAS routines into C++.
This program has unexpectedly come in handy numerous times. For example, when I wanted to fit millions of computer-generated scalar functions to some data, I managed to do it all within a single process. Handy!
Extremely limited. Prototype stage. At the moment, this CAS engine can basically evaluate scalar functions using floating-point numbers. Support for higher symbolic manipulations is limited to a few generic graph re-ordering routines. PolyCAS can optimize scalar functions (see example below) and generate arbitrary expressions by generating arbitrarily valid parse trees. PolyCAS also understands rudimentary binary statements (n.b. not binary inputs, but rather statements that evaluate to a binary value).
The source is available here, and is released in three parts under GPLv3, LGPLv3, and FDL licenses.
Here are some of the example programs (note these are included in the git repository; there are others not shown here):
#####################################################
# Simple numerical evaluation for the shell.
#####################################################
$ ./polycas_evaluate '1+2+3+4+5'
15
$ ./polycas_evaluate '1+2+3+4*5'
26
$ ./polycas_evaluate '1-2*3*4*5'
-119
$ ./polycas_evaluate '1-2*3*4/5'
-3.8
$ ./polycas_evaluate '1-2*3*4/5.1'
-3.70588
$ ./polycas_evaluate '1-2*3^4/5.1'
-30.7647
$ ./polycas_evaluate '1-2*3^exp(4/5.1)'
-21.2002
$ ./polycas_evaluate '1-2*3**exp(4/5.1)'
-21.2002
$ ./polycas_evaluate '1<2'
1
$ ./polycas_evaluate '2<1'
0
#####################################################
# Perform some numerical and benchmark tests.
#####################################################
$ ./test_numerical
--(I) In function: main: The input is: -----> '1.000+3E-1-0.5*sin(1.2345678)*cos(1.45678)/0.5'.
--(T) File: Test_Numerical.cc, Line: 24 Initialized timing marker.
--(T) File: Test_Numerical.cc, Line: 26 Time since last call: 0.000646114 seconds
--(I) In function: main: Validation was OK.
--(I) In function: main: Simplification was OK.
--(T) File: Test_Numerical.cc, Line: 47 Time since last call: 0.000335932 seconds
--(T) File: Test_Numerical.cc, Line: 51 Time since last call: 2.18719 seconds
--(I) In function: main: The numerical evaluation was OK. The result was: 1.1926.
--(I) In function: main: Test was successful.
#####################################################
# Fitting a user-defined 1D scalar function to data.
#####################################################
$ ./test_fitting_1
--(I) In function: PolyCAS_Fit_Data: Minimization: At iteration 1 the lowest value is 20.63241838.
...
--(I) In function: PolyCAS_Fit_Data: Minimization: At iteration 51 the lowest value is 20.63222437.
--(I) In function: PolyCAS_Fit_Data: Minimization: At iteration 52 the lowest value is 20.63222435.
--(I) In function: PolyCAS_Fit_Data: Min scheme completed due to ftol < ftol_min..
-6 1.6
-5 1.8
-3 2
0 4
2 2.75
3 1.68
4 0.64
6 0.2
chi_sq = 20.63222403
Qvalue = 0.0009504217512
DOF = 5
red_chi_sq = 4.126444805
raw_coeff_of_deter = 0.8092236477
mod_coeff_of_deter = -1.119737247
a=3.66702
x0=-0.808536
b=3.15701
a*exp(-0.5*((x-x0)/b)^2)
#####################################################
# Fitting a user-defined 2D scalar function to data.
#####################################################
$ ./test_fitting_2
1 1 3
2 1 3.1
3 1 3.2
4 1 3.4
1 2 4
2 2 4.2
3 2 4.3
4 2 4.5
1 4 5.4
2 4 5.6
3 4 6
3.5 4.1 3
chi_sq = 7.39824
Qvalue = 0.595731
DOF = 9
red_chi_sq = 0.822026
A=-0.105686
B=0.343303
C=3.27938
A*x+B*y+C
#####################################################
# Generate valid algebraic expressions using user-defined primitives.
#####################################################
$ ./test_generation
(-S1y)
(-(S1y*S1y))
(-S1y)
(-(Sb-(-S3m)))
((S1y+Sb)-(Sb/(-Sb)))
((S3m-S1y)/S1y)
((Sb/(-Sb))/S3m)
(-(-Sb))
(S1y+S3m)
(-(Sb-Sb))
(S1y/(S3m*S3m))
(S3m*(Sb-(S1y/(Sb/S1y))))
...
Please send questions, comments, or pull requests here.