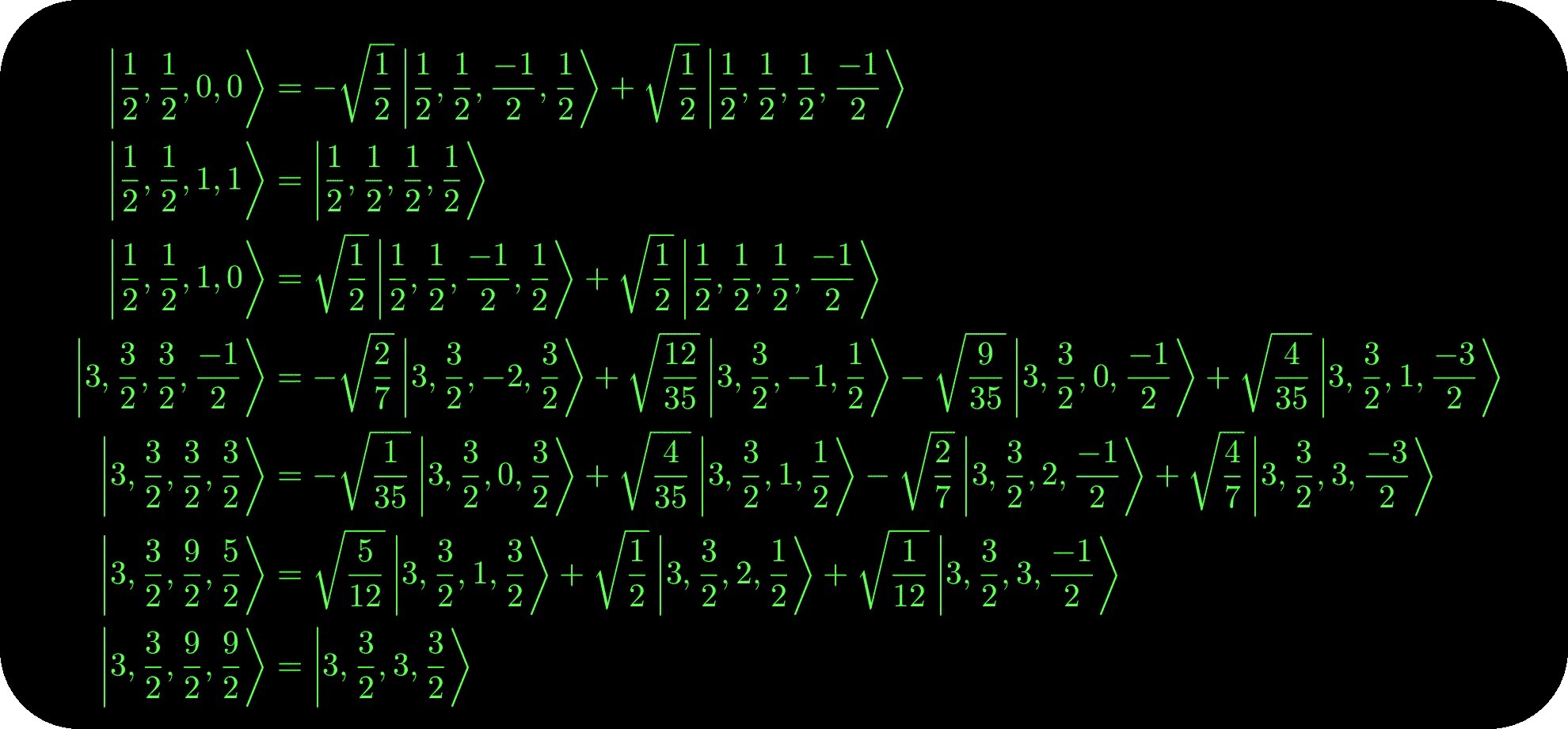
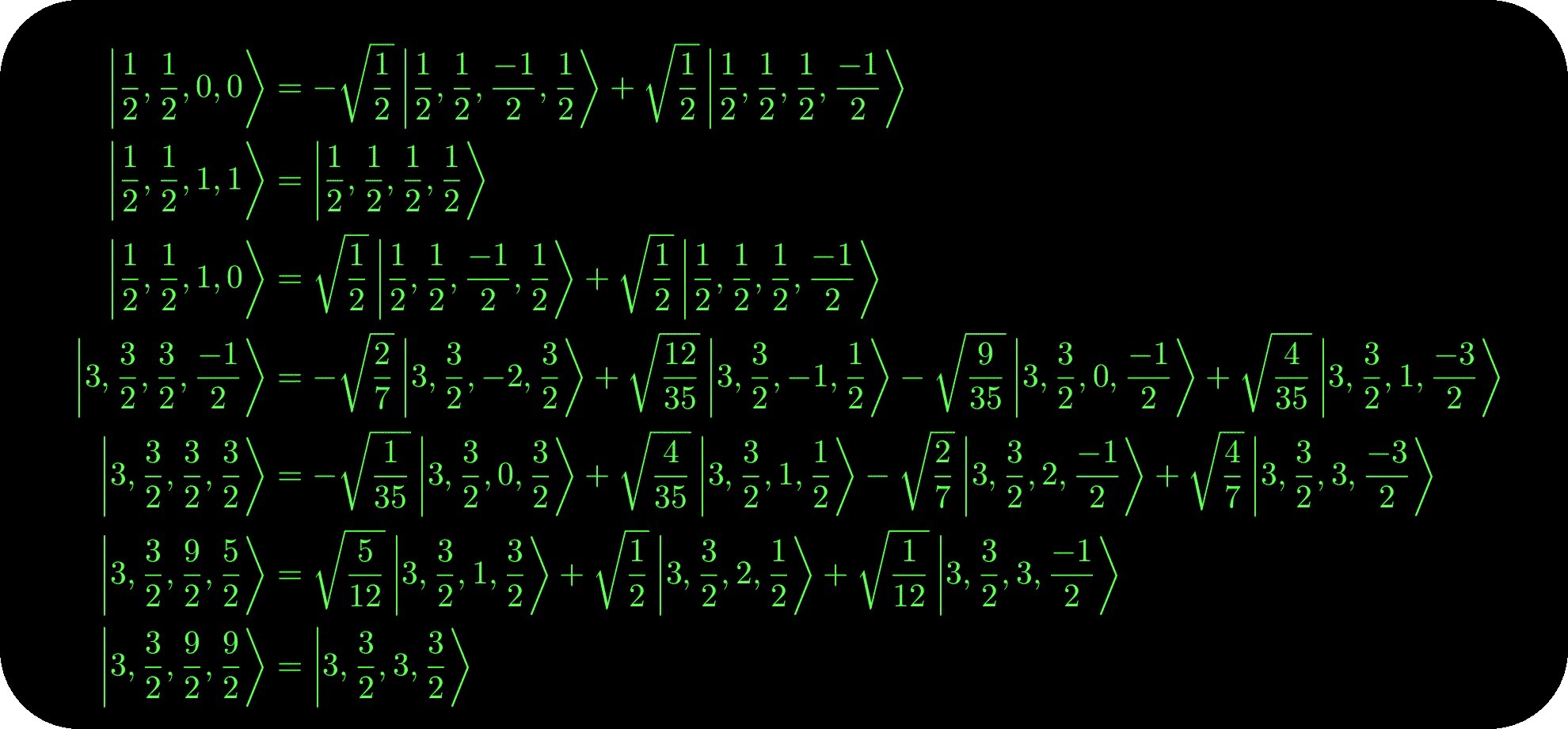
Compute Clebsch-Gordon Coefficients in a self-contained, minimal C++ program.
Wikipedia (at the time of writing) describes Clebsch-Gordon coefficients as:
... [appearing] as the expansion coefficients of total angular momentum eigenstates in an uncoupled tensor product basis. In more mathematical terms, [they] are used in representation theory, particularly of compact Lie groups, to perform the explicit direct sum decomposition of the tensor product of two irreducible representations (i.e., a reducible representation) into irreducible representations, in cases where the numbers and types of irreducible components are already known abstractly.
Results are output in exact form (square roots of rational numbers) and in either an on-screen (human parseable, computer non-parseable) format, or in LaTeX code (computer parseable, human non-parseable).
This program is not very efficient, and can be quite slow for large coefficients. There are faster ways to compute Clebsch-Gordon coefficients, but I’ve never needed any that this program could not compute in a few seconds. Furthermore, Clebsch-Gordon coefficients are often not needed explicitly, because one can work out the decomposition indirectly. On the other hand, sometimes it’s more convenient to simply compute them.
The code should be understandable. There are inline comments (examples below) showing what is happening. I have no immediate plans to continue development, and am not currently using it for research.
This program is released under GPLv3, and FDLv3 licenses. All sources are available here.
Here are a listing of some coefficients for up to spin-4 particles:
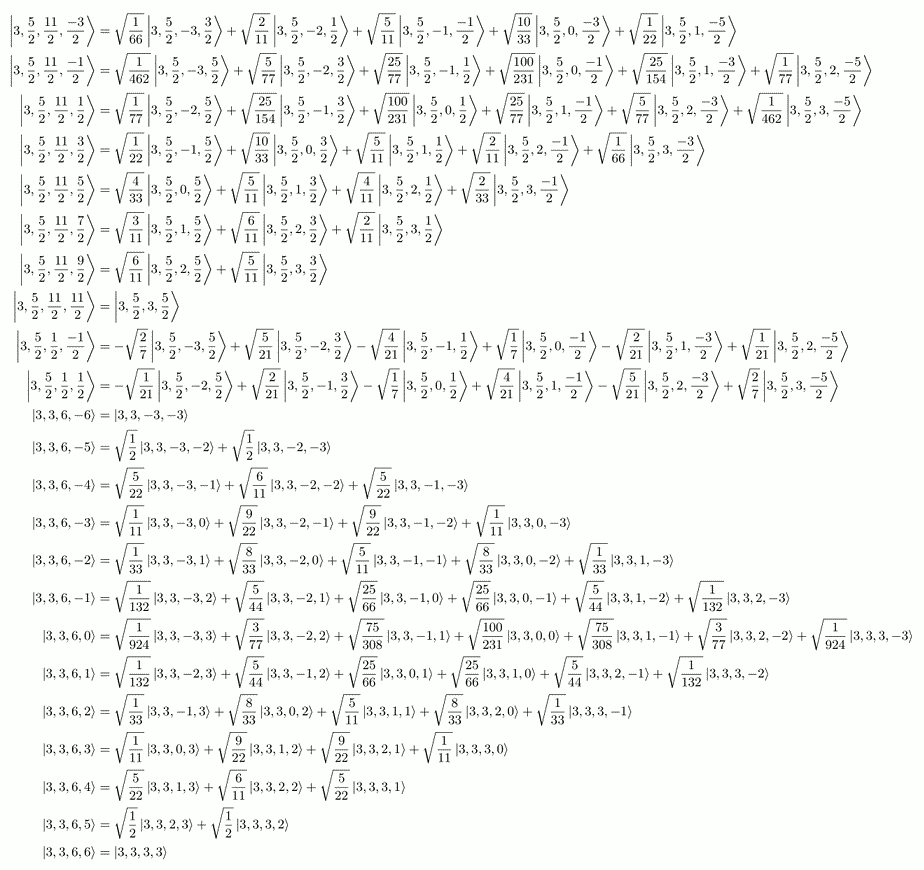
The full LaTeX output for up to spin-4 particles compiled into a PDF is here. Note this listing is licensed cc-by-nc-sa-3.0.
Here is an example of the commented code:
...
//Step 1) Determine the maximum m1 value possible.
frac m1_max = j1.abs();
//Step 2) Determine the maximal m2 value with m1 at maximum.
frac m2_max = (j - m1_max);
//Step 3) Determine the minimum m1 value possible.
frac m1_min = -j1.abs();
//Step 4) Determine the minimal m2 value with m1 at minimum.
frac m2_min = (-j - m1_min);
//Step 5) Set the value of the (m1_max,m2_max) CGC coefficient
// to be 1. No shenanigans here with m (m = m1 + m2.)
std::vector<frac> arb;
arb.push_back( frac(1,1) );
TheCoeffs[CGCcoeff(j1, j2, m1_max, m2_max, j, m1_max+m2_max)] = arb;
//Step 6) Starting at (m1_max,m2_max-1), use the J- relation to
// determine the coefficient (m1_max,m2_max-1) in terms of
// (m1_max,m2_max) and a known (or zero) term to the right.
// If one cannot be determined, indicate so.
for(frac m2 = (m2_max-1); m2 >= -j2; --m2){
std::vector<frac> PreFactorsA;
// J- equation: What are A,B,C factors?
//
// m2| C
// | o (m1, m2+1) x x
// | |
// | |
// | |
// | |
// | |
// | |A B
// | o-------------o x
// | (m1,m2) (m1+1,m2)
// |
// ---|----------------------------------
// | m1
// |
frac m = m1_max + m2 + 1; //Comes from the use of J- on the state.
frac A = (j + m )*(j - m + 1);
frac B(0,1); // = (j1 - m1_max)*(j1 + m1_max + 1); //Always zero here.
frac C = (j2 - m2)*(j2 + m2 + 1);
if(A == 0){
//If A is ever zero, then we have an issue. Report it and then sepuku!
std::cerr << "Found a troublesome zero in step 6. Tell the human to fix me." << std::endl;
exit(0);
}
//Get the prefactors from the point above (the point denoted C.)
std::vector<frac> PreFactorsC = TheCoeffs[ CGCcoeff(j1,j2,m1_max,m2+1,j,m) ];
PreFactorsA.push_back( (C/A)*PreFactorsC[0] ); //Only one number to worry about here.
if(PreFactorsA.size() != 0) TheCoeffs[ CGCcoeff(j1,j2,m1_max,m2,j,m-1) ] = PreFactorsA;
}
//Step 7) Use the J+ relation to determine (m1_max-1,m2_max) in
// terms of (m1_max,m2_max) and (m1_max,m2_max-1).
//Step 8) Perform the previous step but with m1_max decremented.
// Continue this until m1_max-i == m1_min.
for(frac m1 = (m1_max); m1 > m1_min; --m1)
for(frac m2 = (m2_max); (m2).abs() <= j2; --m2)
if( (-j <= (m1-1+m2).abs()) && ( (m1-1+m2).abs() <= j ) ){
std::vector<frac> PreFactorsB;
// J+ equation: What are A,B,C factors?
//
// m2| B A
// | o-------------o (m1,m2) x
// | (m1-1,m2) |
// | |
// | |
// | |
// | |
// | C |
// | x o x
// | (m1,m2-1)
// |
// ---|----------------------------------
// | m1
// |
frac m = m1 + m2 - 1; //Comes from the use of J+ on the state.
frac A = (j - m)*(j + m + 1);
frac B = (j1 + m1)*(j1 - m1 + 1);
frac C = (j2 + m2)*(j2 - m2 + 1);
if(B == 0){
//If B is ever zero, then we have an issue. Report it and then sepuku!
std::cerr << "Found a troublesome zero in step 7. Tell the human to fix me." << std::endl;
exit(0);
}
//Get the prefactors from the local point (point A) and the one below (point C)
// so we can determine the prefactor for the point to the left (point B.)
std::vector<frac> PreFactorsA = TheCoeffs[ CGCcoeff(j1,j2,m1,m2,j,m+1) ];
std::vector<frac> PreFactorsC;
if( (m2-1).abs() <= j2 ) PreFactorsC = TheCoeffs[ CGCcoeff(j1,j2,m1,m2-1,j,m) ];
for(size_t i=0; i<PreFactorsA.size(); ++i) PreFactorsB.push_back( (A/B)*PreFactorsA[i] );
for(size_t i=0; i<PreFactorsC.size(); ++i) PreFactorsB.push_back( -(C/B)*PreFactorsC[i] );
if(PreFactorsB.size() != 0) TheCoeffs[ CGCcoeff(j1,j2,m1-1,m2,j,m) ] = PreFactorsB;
}
...
Please send questions, comments, or pull requests here.